|
ALS-XZ Rule
Points. 2 Almost Locked Sets with a restricted
common digit X will cause eliminations for other common digits Z.
The ALS-XZ rule says that if A
and B are two Almost Locked Sets, and X is a restricted common to A and B, then
no other common candidate, Z, can appear anywhere outside of A and B that
can see all the Z candidates in both A and B. Note that Z can also be a
restricted common to A and B nad cause further eliminations. i.e, each
restriced common is considered seperately.
|
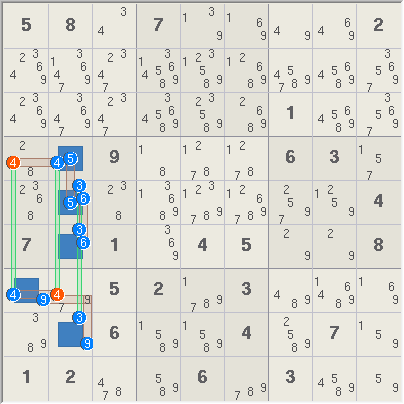
Example 1, has two
ALS: r4568c2 (4 cells) with digits 3,4,5,6,9, and r7c1 (1 cell) with digits
4,9. Digit 9 is a restricted common X to both sets. All candidates for
digit 9 in each set lie within box 7 and can thus see each other. This box
can have only one digit 9, so one of the sets will not contain digit 9.
Digit 4 is a Z digit because it is also present in both sets. Because
digit 9 can exist in only one of the sets, digit 4 must be in the other,
which ever set that is. Either way, digit 4 cannot be in r4c1 and r7c2.
|
|
|
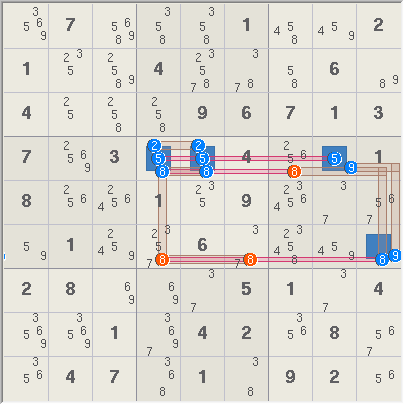
Example 2. Two ALS:
r4c45 (3 cells) with digits 2, 5, 8, 9, and r6c9 (1 cell) with digits 8 and
9. Digit 9 is a restricted common X to both sets. All candidates for digit
9 in each set lie within box 6 and can thus see each other. Digit 8 is a Z
digit because it is also present in both sets. The three red digit 8s can
thus be removed.
|
|
|

