Locked Candidates
Points.
Locked Candidates is a single digit method where all
candidates in one line/box are located in a three-cell intersection with
another box/line. Digits outside the intersection can be removed from the
second set, the covering set. Locked candidates are pointing if the
first set is a box, or claiming if not
|
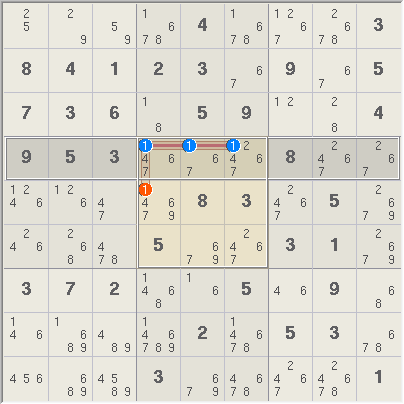
Locked Candidates, Claiming, Rows. The three candidates in row 5 make a truth that is covered by box 5, thus the red candidate can be removed. The row containing the truth is shaded gray
and the box is shaded yellow.
|
|
|
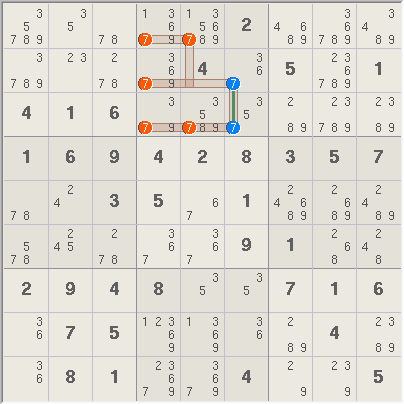
Locked Candidates, Claiming, Cols. The two candidates in column 6 make a truth that is covered by box 2, thus the 5 red candidates can be removed from the box.
|
|
|
Locked Candidates, Pointing, Row. The two digit 1 candidates in box 5 form a truth that is covered
by row 5, thus the 2 red candidates in row 5 can be removed.
|

|
|
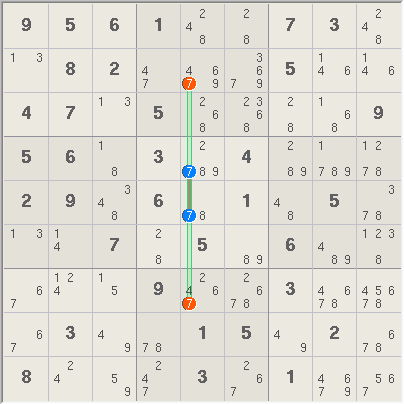
Locked Candidates, Pointing, Cols. A pair of digit 7 candidates in box 5 form a truth that is covered by column 5, thus the 2 red candidates in column 5 can be
removed.
|
|
|



