|
Welcome
to SudokuOne.Com Goto ==> SudokuOne
Homepage
Easter Monster
Easter Monster, below, is one of the toughest known puzzles with an almost symmetrical crisscross pattern typical many monsters. Steve's logical method produces a first stage solution whose simplicity contrasts with the puzzle's difficulty. Part of the simplicity is due to the puzzles symmetry.
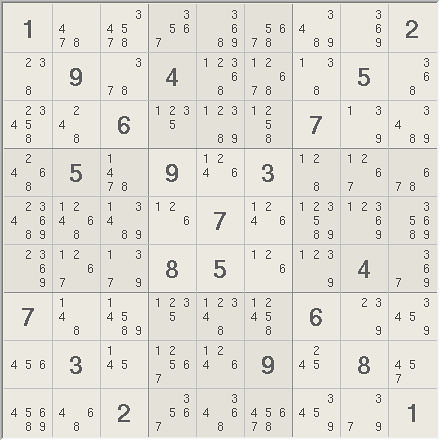
Rank 0 Solution
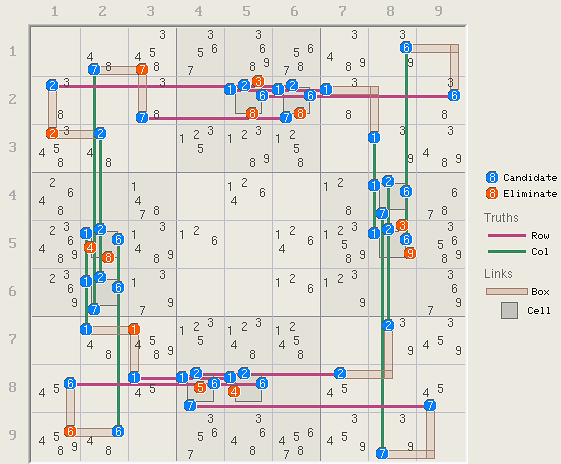
The solution structure has 16 sets and 16 linksets where 12 sets have three candidates each and the rest have only two. These 32 sets form a fully linked rank 0 structure with no overlapping sets or linksets. The structure is multi-looped like a common rank 0 fish or perhaps a swordfish because the largest sets have only three candidates. A total of 13 candidates are eliminated from link sets. The loop with eliminations are shown here.
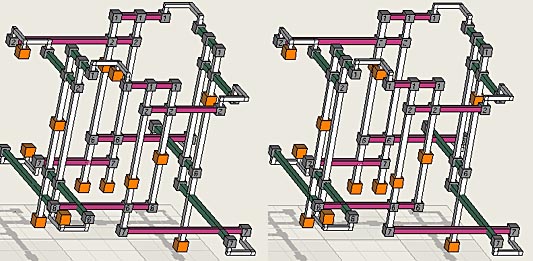
Stereoscopic 3D view of SK-Loop The
SK-Loop is so symmetrical it is worth the effort to view it in its full 3D
beauty. Below is a stereoscopic image of the SK-Loop in 3D. Instructions: Look at the screen holding an A4 or
letter size piece of paper between your eyes, long way, so the left eye sees
only the left image and the right eye sees only the right image. Now relax
your eyes, or think about focusing your eyes on a distant object, like a
mountain. Slowly the two images should come together and you will see one
single stereo 3D image.
Early 3D Photography A
bit off topic, but early 3D photography dates back to the 1850s!. Here is an
early image of a procession in London, England. Use the same proceedure used
above to see the stereoscopic view.
Logical Sub-Units
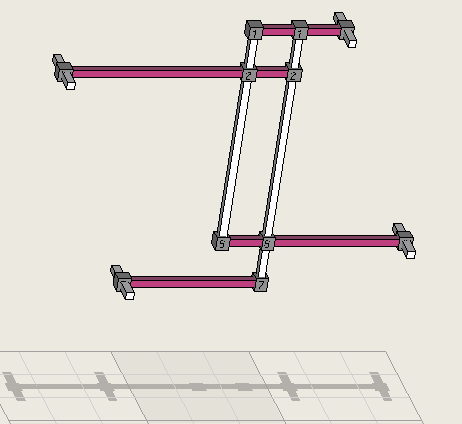
An interesting point is that the solution was found by building a logical structure from a number of identical equivalent. The loop can be made from eithr 8 two-set units or 4 four-set untis. Below is one of two row subunits. There are an additional 2 column subunits. The four-set subunits are generally called AAHS and have a rank of 2.
The subunit seen sideways in 3D. .
|