|
A General Sudoku Logic Odd Loops, Broken Wings, and Dark Logic |
|
Points.
Odd length loops are present in many solving methods such as chains and
dis-continuous nice loops. The broken wing method eliminates candidates by
using the fact that odd length loops of strong links cannot occur in a valid
puzzle. This method can be generalized using sets and represents a
fundemental principle in Sudoku set logic.
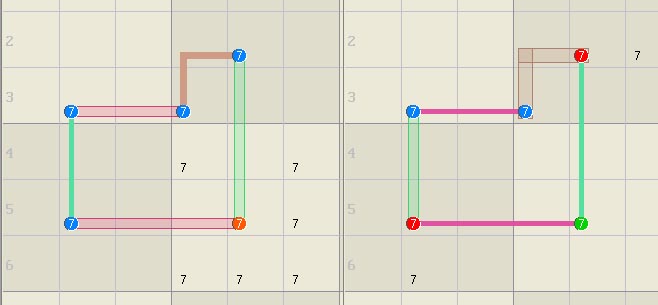
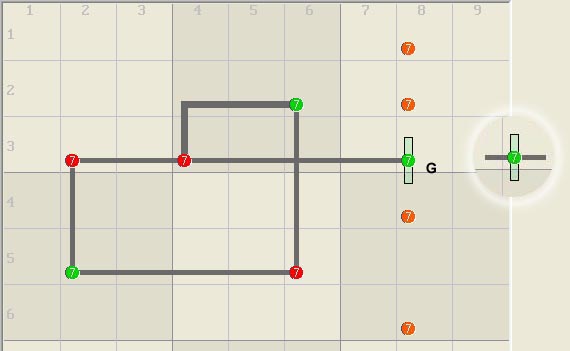
Odd Length Loops Many Sudoku solving methods are based on odd length
loops. The simple chain example below left has 5 links and a target candidate
(red) at the intersection of two linksets, r5c5. With a different set of
strong links (right), the same nodes form a discontinuous nice loop that
assigns the target candidate rather than eliminate it.
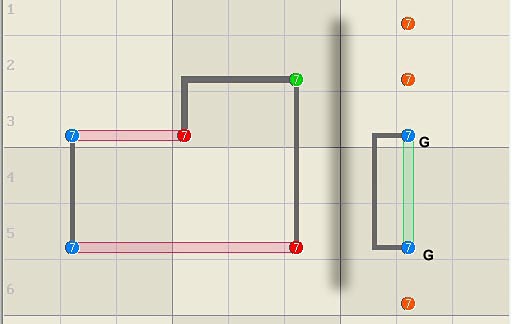
Illegal Logic and Rank Illegal logic is any group of sets (or candidates)
that has no solution, i.e., there is no way to arrange the candidates that is
allowed by the rules. The illegal 'fish' below has 3 sets connected by two
linksets where it's easy to verify that 3 candidates
cannot be placed in 3 sets without placing 2 in a single linkset. The illegal
structure, denoted by black sets, has a rank of 2 linksets - 3 sets, which
equals minus 1.
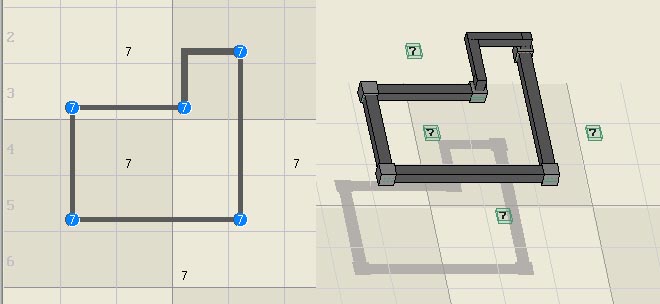
Odd length loops of bi-value strong links are also
illegal. The length 5 loop below can contain at most two nodes without double
occupancy, which leaves one set unoccupied. Loops of any odd length have a
rank of minus 1.
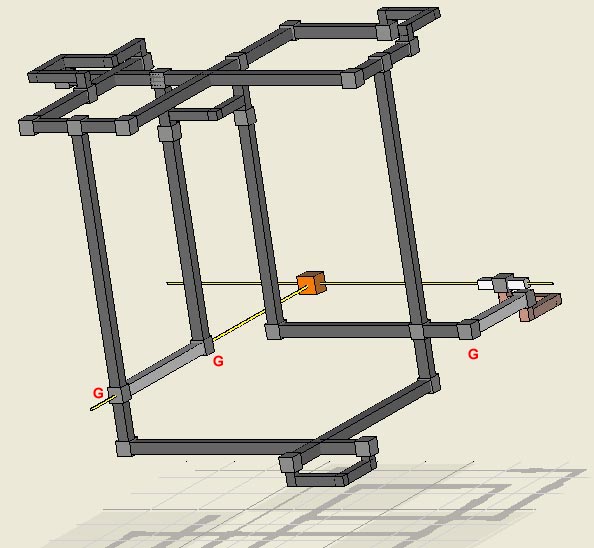
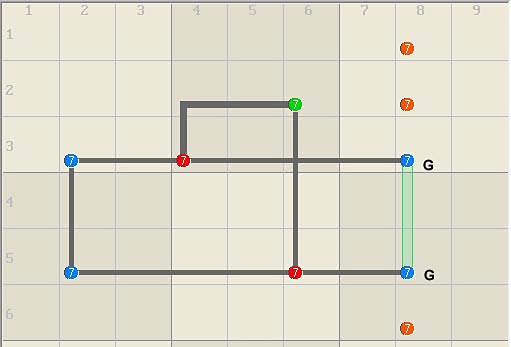
Broken Wings Broken Wing is a unique method that has been widely
applied. It assumes that a valid puzzle cannot contain loops with an odd
number of bi-value strong links (conjugate
pairs). To be legal, at least one link
must contain at least one extra candidate, called a guardian. If there is one
guardian, it can be assigned. If there are multiple guardians, eliminations
can be logically deduced. Guardians can be connected to a variety of logic. The lone guardian (G) in r3c8 below prevents the logic from being
illegal and is thus assigned becoming a single. It then eliminates the
orange candidates in column 8. Additional assignments and eliminations are
explained later.
Broken Wings and Dark Logic Broken wings occur naturally in set logic along with
other odd length, strong-set logic. The following is a simple set logic view
of broken wing principles that applies to a wide range of logic. In terms of
set logic, the broken wing principle is both unique and elegant. The same
principles can be applied to deadly patterns and URs. To keep track of what's
what, the term dark refers to anything illegal caused by odd
length loops. A dark loop contains the sets
and nodes belonging to illegal logic but not guardians or other logic that
may be in the same sets. Defined this way, dark loops have the following
properties: A
dark loop of any size has a rank of minus 1 and is outside of the set
and linkset groups that determine eliminations in the rest of the logic
(according to set theory) A
dark loop can be removed and the remaining candidates, such as guardians,
placed in a virtual set that behaves like ordinary sets. This virtual set can
span rows, columns, and boxes. In short, a broken wing is made of a dark loop plus
guardian candidates, all contained in the same sets. The dark logic disappears
(sets and nodes) leaving behind the guardians that act as if they were in one
virtual set. (Why?, becasue of the dark force,
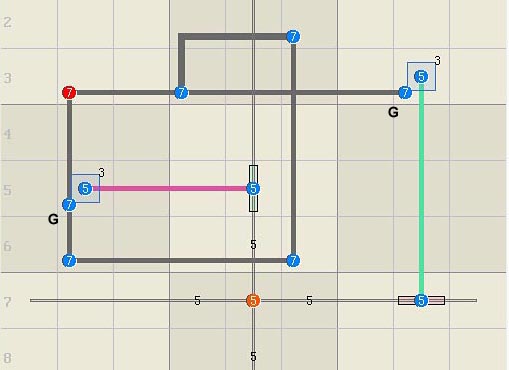
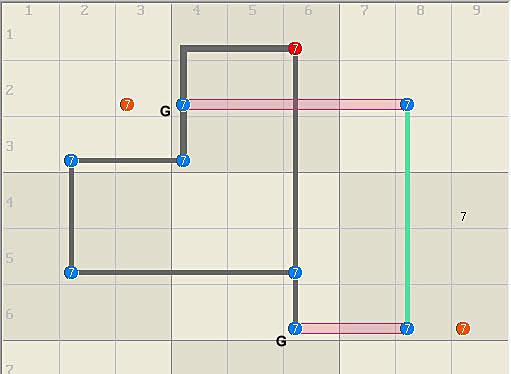
of course.) Below is a two-guardian broken wing. Although
neither guardian can be assigned, one must be true so the linkset in column 8
is always occupied, or rank 0, which eliminates the
red candidates.
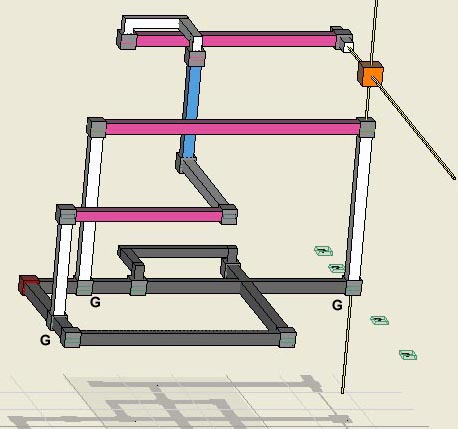
From the set logic view, the dark loop's guarantee
of one true guardian effectively divides the problem in two. On the right,
the guardians now work as if they are in a single virtual set, which forms
something like locked candidates, except it spans 2 boxes. On
the left, the guarantee of one true guardian means that rows r3 and r5 are
linksets for the dark loop, which is solved in the normal way as a
discontinuous nice loop that assigns 7r2c6, thus eliminating the two red
candidates.
Implications There must be a large number of odd length loops in
every Sudoku grid, each of which can be broken into a dark loop and a virtual
set. A set logic solver could first catalog these virtual sets and add them
to the set base when searching for logic. Something similar could probably be
done with other solvers. The same principles can be applied to deadly
patterns and unique rectangles, which also require at least one additional
candidate to be legal. The deadly patterns can be removed and the remaining
candidates from their sets placed in a virtual set. The only difference is
that broken wings are naturally illegal while deadly rectangles are illegal
by the convention that valid puzzles have one solution. Examples Below is a chain is made of 4 linksets and 3 sets including
the virtual set in the middle of the chain. In set terms, the dark loop is
replaced by virtual set V making the chain: c55-(r55)-n52-(V)-n38-(c85)-r75
=> r7c5 <> 5 where sets are in ( ) and linksets are not. Written as a
chain: 5r7c5-5r5c5=5r5c2-7r5c2=V=7r3c8-5r3c8=5r7c8-5r7c5 => r7c5 <> 5 Set r37 is then a linkset and the dark loop is
solved as another chain: 7r3c2-7r3c4=7r2c6-7r6c6=7r6c2-7r3c2 => r3c2 <> 7
This X-wing has a set in column 8, a virtual set
from 7r2c4 to 7r6c6, and linksets in rows 2 and 6, which eliminate candidates
7r2c3 and 7r6c9.
The 3D Kraken fish, shown in 3D, has 5 sets,
including the dark loop, 6 linksets, and a rank of 1. The virtual set has 3
candidates. The loop sits vertical with the virtual set on the bottom and the
middle red row set on top.
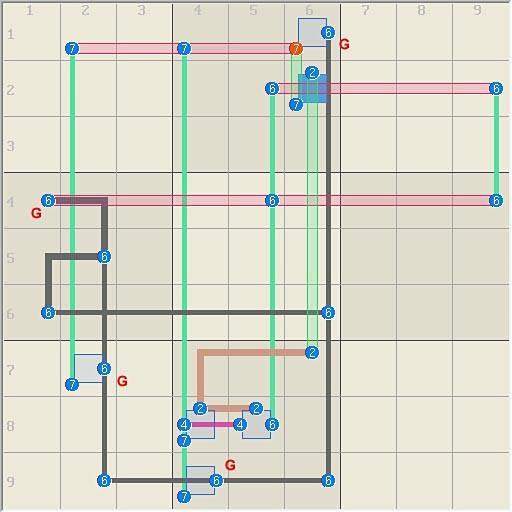
Complex Examples The dark logic principle should work with any logic
as long as the dark logic nodes do not link to the the rest of the logic,
even then the principle still applies This example has 12 sets, 10 linksets,
and a 5 set dark loop that is replaced by virtual set V. The replaceable sets
are in red and the set logic is given
by: S-12 = [r84 r66 r96 c26 c66 c(59)6 c(24)7 n26 b46 b82], L-10 =
[r(24)6 r17 c6(27) n16 n72 n8(45) n94] Substitute V1
=> S8=[V r84 c(59)6 c(24)7 n26 b82], L10=[r(24)6 r17 c6(27)
n16 n72 n8(45) n94] =>
r1c6<>7 The logic now has 8 sets, 10 linksets. It is
therefore 2 so thus 3 overlap linksets are needed to
eliminate a candidate. Linksets r17, c67, and n16 overlap at cell r1c6 to
eliminate candidate 7r1c6.
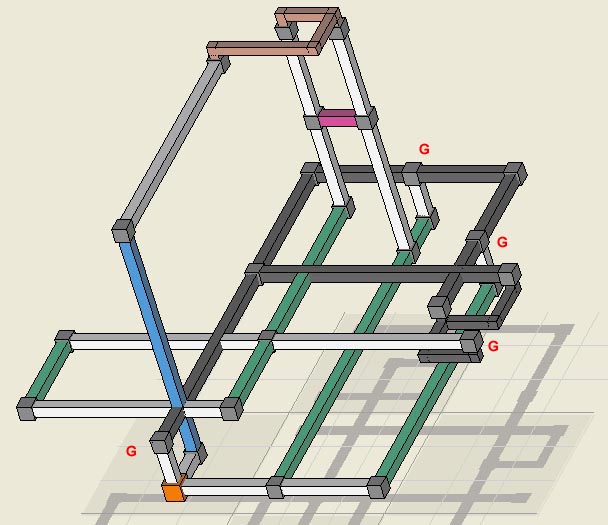
Three dimensional view of the above logic example.
Another extreme example below comes from Easter
Monster. It has 3 linksets and 18 sets of which 17 are linked into one great
piece of dark logic. There are 3 guardians but two are in the same linkset.
The logic is thus 2 sets + 3 linksets => rank 1, or a simple chain. The
dark logic acts like a box or a hinge because it place puts guardians in the
same linkset. The two linksets at the ends of the chain overlap to eliminate
the orange candidate.
|
 .
.