|
Welcome
to SudokuOne.Com Pluralitas non est
ponenda sin neccesitate A General Logic for Sudoku |
|
Also
see details seen in images. Sudoku is defined in terms of its rows, columns, boxes, and cells, each of which must contain a unique value. These are sometimes referred to as the original 324 constraints or sets of candidates. General logic is a way of reasoning based on these rows, columns, etc. The basic ideas of general logic are not new and are used in several Sudoku methods such as fish, naked/hidden multiples, etc. General logic starts with the basic idea of base sets that are truths, and cover sets that are links. It then extends these ideas in different ways to create a set of common rules that apply to virtually all Sudoku methods. The evolution goes something like this. ·
A rule for N truths covered by N links,
the standard fish method. ·
Allow multiple-digits and treat rows, columns,
boxes, and cells equally. ·
Define a global property called rank
that measures the relative number of truths and covers. · Allow for an unequal numbers of N truths covered by M links. · Allow for multiple overlapping truths and overlapping links. · Include potential illegal logic, which can describe uniqueness, broken wings, and inference sets. Truths and Links A truth is any set of
candidates where one candidate is part of the solution, i.e., a true
cnaididate. Every Sudoku grid has 324 native truths, one truth for each of
the 81 cells and 9 truths for each of the 9
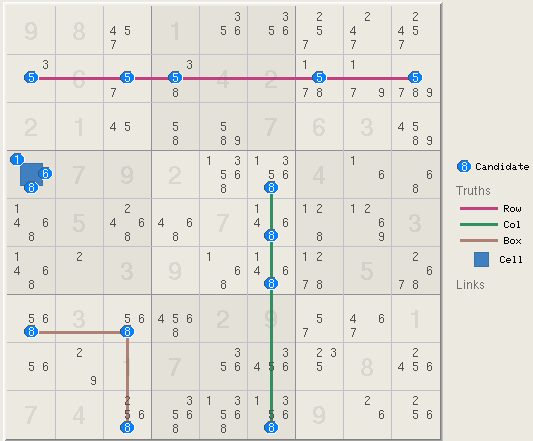
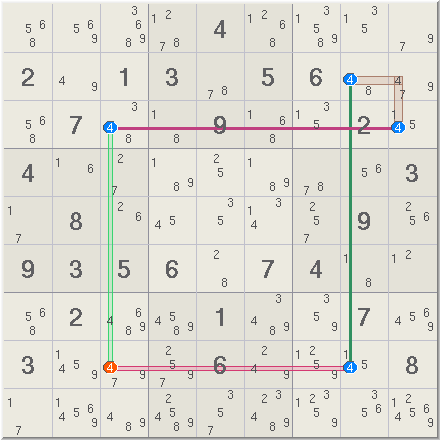
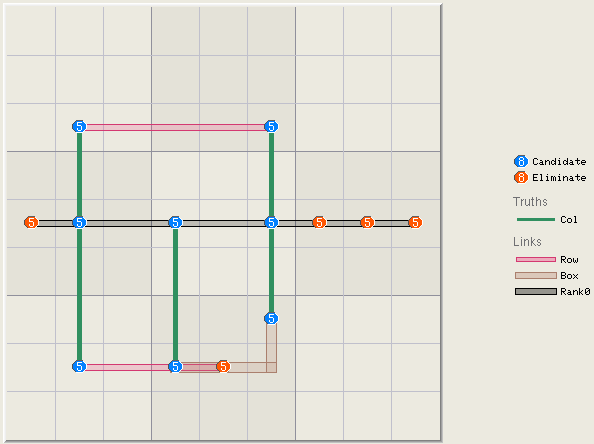
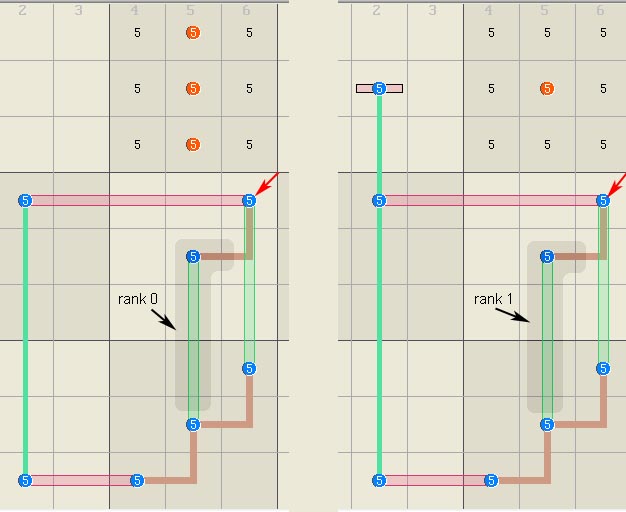
rows, columns, and boxes. Row 2 below must have a digit 5 thus one of the
five 5s connected by the red line must be true. The red line is therefore a truth.
Row 2 has 9 truths, one for each of the 9 digits. The grid also has one
column, box, and cell truth.
PART 1, Cover Sets and Rank Base
and Cover Sets and Eliminations One
simple approach uses the fact that there is one true candidate in each
base set (truth). The number of true candidates is thus equal to the
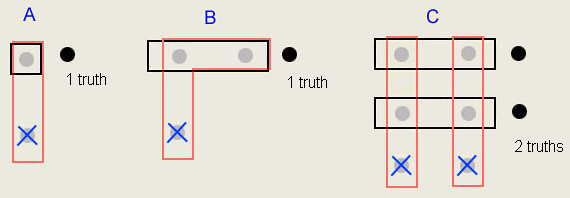
number of base sets (black rectangles below). When all candidates in the base
sets are covered by links (red rectangles), all the true candidates in
the base sets must also be in the links. If
the number of bases is equal the number of links, then every link has a true
candidate from the bases thus any other candidates in the links can be
eliminated (X). This rule holds for any equal number of bases and links. The
only restriction is that the bases cannot overlap. This is discussed below.
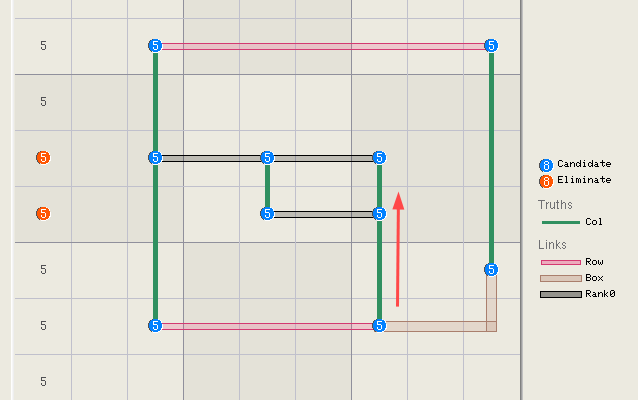
Diagram
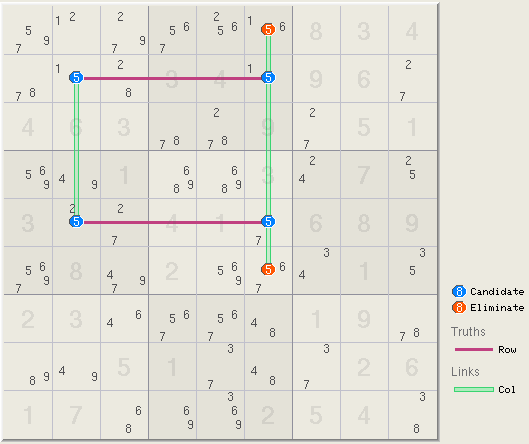
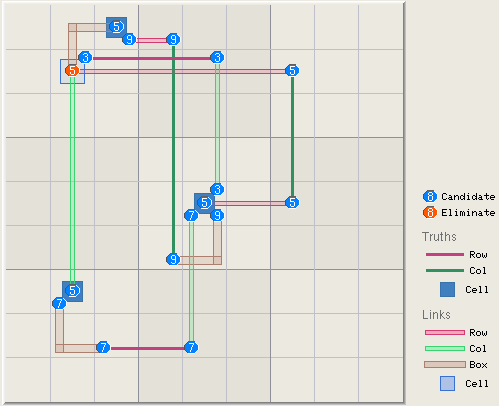
C above is an X-Wing, an example of which is shown in the grid below. The two
truths are located in rows 2 and 5, the links are located in columns 2 and 6.
Rank and Rank 0. It's
useful to define a term called rank where: Rank = number of cover links
- number of bases The
above examples had equal numbers of bases and links and were therefore rank
0. From the aabove we can summarize a
rule for rank 0. Rank 0: Any non-base candidate contained in any link can be eliminated. This
is a general rule that is not restriced to single digits and makes no
distinction between cells, rows, boxes, or columns. The 81 cells are treated
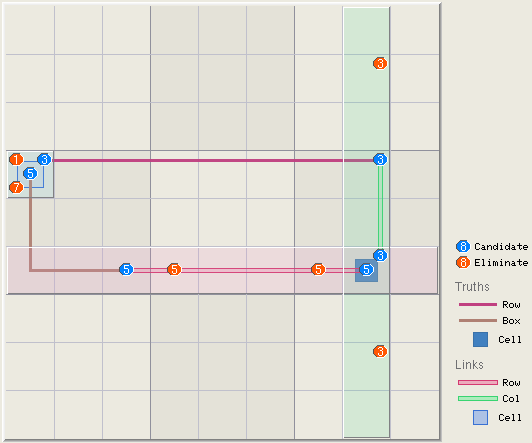
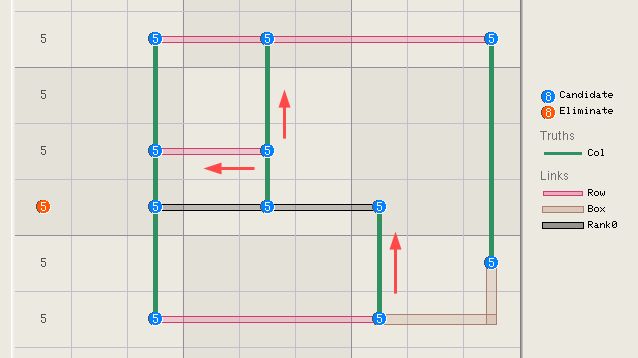
equally to the 81 row-digit sets, etc. This following example logic has 3
truths, 1 row + 1 box + 1 cell. The truths are covered by 3 links, 1 row + 1
column + 1 cell. The rank is 3 – 3 = 0. Accroding to the rank 0 rule,
all candidates in all links can be removed. The links zones in row 6, column
8, and cell r4c1 are highlighted. Any candidates in these zones will be
eliminated.
Rank 1 Rank
1 logic has one extra link thus N sets must have N true candidates
distributed among N+1 links. In this case, any two links are
guaranteed to contain one true candidate from the bases sets, thus anywhere
any two links overlap, outside of the bases, can eliminate candidates. A rank
1 rule would read Rank 1: Any non-base candidate contained in any two links can
be eliminated. Rank
1 logic is common and include chains, finned fish, XY-wings, discontinuous
nice loops, and Kraken fish. A simple rank 1 example below is a crossed
two-string kite.
Rank R The
same general argument holds true for any rank R higher than 1. Rank R logic
has R extra links thus N base sets must have N true candidates distributed among
N+R links. In this case, any R +1 links are guaranteed to contain one true
candidate from the bases sets, thus anywhere any R + 1 links overlap, outside
of the bases, can eliminate candidates. The rank R rule is. Rank R: Any non-base candidate contained in any R + 1 links can
be eliminated. Again,
this is a general rule that applies to any number, type, or combination of sets, links,
candidates, and digits as long as the base sets do not overlap. No other rules or restrictions apply, this is the
law! Rank rules apply beyond Sudoku to problems of any geometry and any
number of spatial dimensions. Sudoku is limited to 3 dimensions and 4
overlapping sets. Ranks
0 and 1 cover many Sudoku methods. Ranks higher than 3 possible in complex
eliminations when combined with triplets, described later. The rank 3 example
below has 7 bases covered with 10 cover links. According to the rank rule, 4
covers must overlap to eliminate a candidate. The logic has 4 independent
bi-value paths emerging from the cell set in r5c5. The 4 branches converge at
5r2c2 where they eliminate the red candidate.
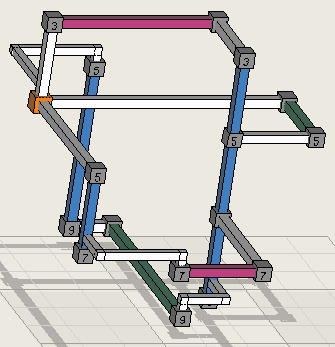
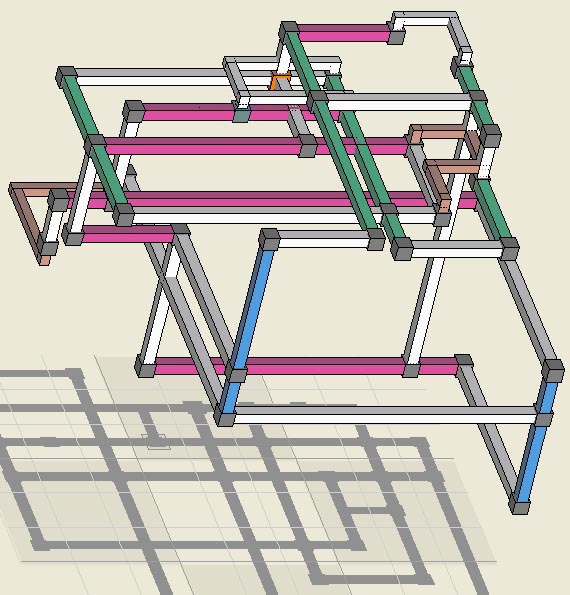
Three-dimensional
view with colored sets and white links. The four links converge on 5r2c2 to
eliminate the orange candidate.
Some rank R examples: rank 2 three leg bug. Illegal Logic and Rank -1 Illegal
logic is any group of sets (or candidates) that has no solution, i.e., there
is no way to arrange the candidates that is allowed by the rules of Sudoku.
The illegal 'fish' below has 3 bases connected by two links where it's easy
to see that 3 candidates cannot be placed in the links without placing 2 in a
single link. The illegal logic, denoted by black sets, has a rank of 2 links
- 3 base sets equals minus 1. Negative rank is real and can be a useful
quantity.
Covering Sets, Eliminations, and Multiple Solutions Covering
sets are the links that exactly cover the base candidates. A group of
covering sets is any group of links containing all candidates in the base sets
where no link can be removed and the candidates remain covered. Covering
sets are not necessarily exact cover sets because they are allowed to overlap.
One group of base sets can be covered by multiple groups of covering sets. A
candidate is eliminated only when it sees other candidates through the same
group of covering sets. In other words, rank rules are based on cover
groups. Eliminations occur when one or more links in the
same group of covering sets overlap to contain a candidate. Overlap linksets
from different cover groups do not cause eliminations. Cannibal Eliminations In
Sudoku, cannibal eliminations occur when a candidates in a base set or other
kind of truth are eliminated. Cannibal eliminations are virtually always
caused by a subgroup of the base and cover sets being considered,
i.e., simpler eliminations exist. Counting Rank When
counting rank or searching for a solution of covering sets, two points are
considered.
PART 2, Triplets and Rank Regions Triplets, Overlap, and Pointing Two
base sets or two links that overlap form a triplet. The left circle below marks a candidate in 2
overlapping bases + 1 link. The right circle marks a candidate in 2
overlapping links + 1 base set. Because the three branches connected to the
triplet are not equal, it's convenient to describe the direction of a triplet
as pointing towards its odd branch. A triplet with two bases points in the
direction of its link and a triplet with two links points in the direction of
its base set. The logic in the pointing direction is called the upper branch.
When sets or links form triplets, they have a global
effect on logic. When two bases overlap, the logic no longer
contains a fixed number of true candidates to occupy the cover links. When
two links overlap, the number of true candidates is
fixed but the number of occupied links is not. Both cases can lead to regions
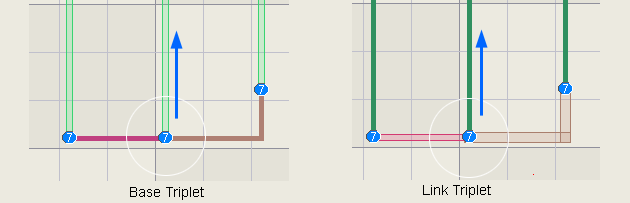
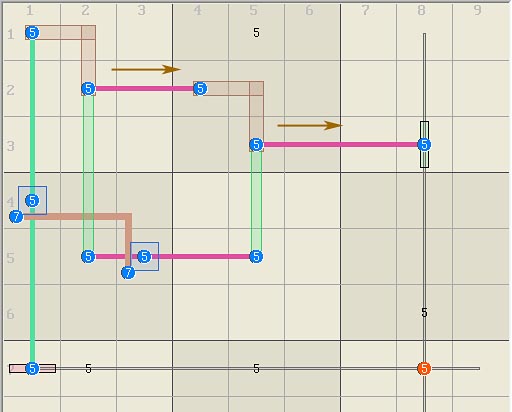
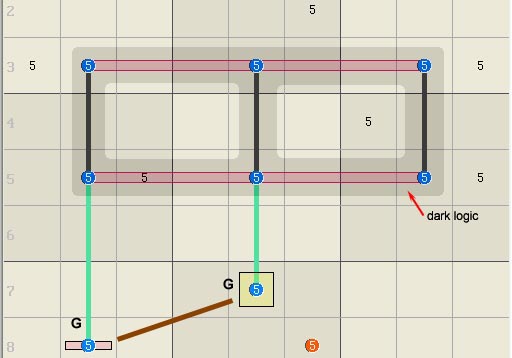
with different rank and novel eliminations or assignments. Base Triplets and Rank When
base truths overlap, the rank must be corrected because the number of true
candidates is no longer constant. The
example below has 3 base sets (2 red rows and 1 brown box) and 3 column links
(light green), and a base triplet. The triplet has only two states, occupied
or not. Un-occupied: When a base triplet is un-occupied (left) there
are 3 true candidates to occupy the 3 links, thus its rank = 0. Occupied:
When a base triplet is occupied (right), the number of true candidates in the logic drops by 1 because the triplet's true candidate occupies 2 bases. Two true candidates in 3 links
means rank 1. However, the triplet's link must be occupied because the
triplet is occupied thus the triplet's link must have a rank of 0. The
worst-case rank for the logic is 1 except for the triplet's link, which is 0.
Eliminations are based on the worst case rank, which is 0
for the triplet's link in column 4. Thus all other digit 5s can be eliminated
from the column. The triplet has
created different rank regions in the logic. The rank 0 region in column 4 is
highlighted black.
Link Triplets Link
triplets are slightly different because the number of true candidates
is fixed but the number of occupied links can vary. This again can lead to
mixed rank logic. The two possible states are shown below where the blue
arrows mark the link triplet. There are several ways to arrange the true candidates
(yellow squares), two ways are shown below.
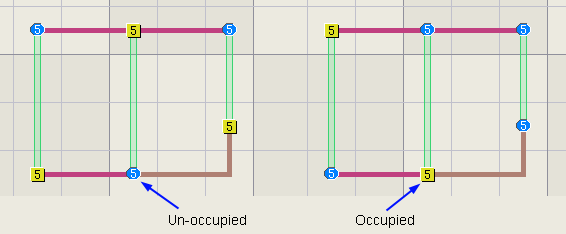
The logical argument goes like this. The overall rank is 1
because the logic has one extra link. Occupied: When
the triplet is occupied (right), the overall logic must be rank 0 because all
links have a candidate. Un-occupied: When
the triplet is not occupied, (left) the overall rank must be 1. However, the
base set connected to the triplet now has fewer candidates to cover, which
effectively lowers the rank in that branch. Once
again, the worst case rank is 1 everywhere except for the middle row link in
r5, which has a worst case rank of 0, thus the digit 5 can be eliminated from
that row. The rank 0 link in row 5 is highlighed black. However,
that's not the end of the story. The worst case rank for the other 3 links is
1. According to the rank rules, anywhere 2 of these links overlap can
eliminate candidates. Note that the row and box links in row 8 do overlap in
cell r8c5, where they eliminate the red candidate for digit 5. Thus, this
example has both rank 0 and rank 1 eliminations.
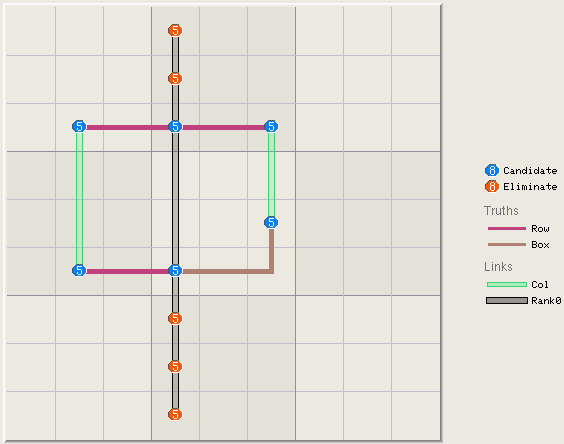
Link Triplets, Example 2 A
link triplet lowers the rank of the of all linksets along its minor branch,
or the set side. The example below has 2 linksets in the minor branch, both
of which are rank 0 (black highlight) and both eliminate candidates on the
left.
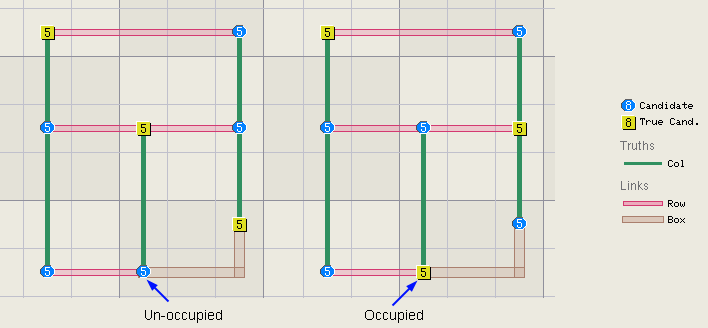
Rank Regions Both
kinds of triplets define boundaries between two regions. For a link
triplet, one region contains the base set branch and the other contains the
two link branches. If the logic on the base side never rejoins the rest of
the logic then the rank will be lower everywhere along the branch. If the set
branch does reconnect, then another boundary is needed to define the region. As
a rule of thumb, the lowered rank branch usually continues until the
first bifurcation that has two separate return paths back to the triplet. The
example below is similar to the one above except now for the bifurcation at
r5c5 that has two separate return paths to the triplet's links thus r5 is no
longer rank 1.
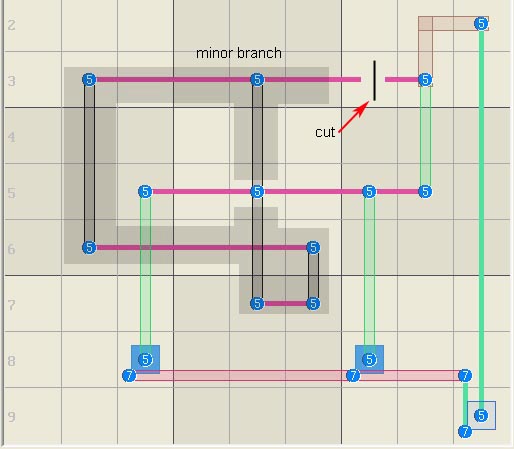
This
bifurcation can be hard to spot as in the next example below with 8 sets, 9
linksets and a rank of 1. A simple way to find the low rank region is to cut the
triplet node from the minor branch, then follow the branch to find those sets
that can be covered by an equal number of linksets, e.g., make a new, small
rank 0 logic block. If the logic was rank 2, then find N sets covered by N+1
linksets along the branch. The minor branch below (dark highlight) has 3 sets
and 3 linksets that make a rank 0 upper branch. Row r5 and its candidates are
not included. This upper branch is a swordfish or fishy cycle. This
procedure works because cutting the branch is the same as assuming the
triplet is not occupied and the upper branch is occupied, which is how the
triplet rule is derived. For a set triplet, cut the triplet from its 2 two
linksets sets leaving the triplet in the minor branch as a single. This is
the same as assuming the triple is occupied.
Rank 2 Mixed Rank Logic Mixed
rank logic can have any rank. The link triplet example below, left has 3
sets, 4 links, and is rank 1. The triplet's minor branch includes the middle
column linkset, which is rank 0 (dark highlight) and has yellow elimination
zones along the column eliminating 1 candidate (red). The example on the
right includes an extra candidate and linkset in row 2, which makes the logic
rank 2. According to the rank rules, the minor branch of triplet r4c6 is now
rank 1 and cannot directly cause eliminations. However, it can eliminate the
candidate at r2c5 by overlapping linkset r25. The linkset to the right of the
branch, c65, also overlaps r25 but cannot cause an elimination because it is
in the rank 2 region.
The Idea of Uniform Rank Uniform
rank over a region seems counterintuitive, especially when thinking about
first order logic however, there is a rational for such an effect based on
permutations of candidates. Given
a rank 1 structure with 10 sets 11 linksets, the cover set principle says any
two linksets must have at least one candidate. This is logically correct but
what makes sure there is always an arrangement of candidates that fulfills
this requirement? Candidates are possibilities. Without constraints, all
permutations or arrangements of candidates are possible, about one billion
for this example. The number is smaller because constraints remove most of
them but without a constraint, or reason not to be there, every combination
is possible. In this sense, the mathematics of combinorics fills all possible
configurations that are not invalid, everywhere in the structure. This
reverses the argument, rather than why should candidate configurations be
there, the correct question is why would they not? In this example, if any
two sets did not contain a candidate, that configuration must be invalid
because it would force two candidates into one of the sets. Additive Properties of Triplets The
effects of triplets can be additive, i.e., two link triplets both aligned in the
direction of a candidate can lower the rank in the region of the candidate by
2. However, such logic must follow the rules about cover sets for triplet
branches. Additively
can be proved using the same arguments used for one triplet, by dividing the problem
into occupied and unoccupied triplet states, the only difference is more
states. Naive arguments for eliminations such as 4 overlap linksets = 2 overlap linksets + 2
pointing linksets triplets can
be helpful but the details of the logic must be considered before accepting
the elimination. The rank 3 logic example below has 5 sets, 8 linksets, and 2
link triplets, 5r2c2 and 5r2c5, pointing in the direction of the candidate.
This adds up to the equivalent of 4 overlap linksets required to eliminate the
candidate 5r7c8. Note that other digit 5 candidates also sit at the overlap
of various linksets, but they are not eliminated.
Very Complex Logic Very
complex eliminations only occur in the most difficult eliminations from the
most difficult monster puzzles. The following elimination from Easter Monster
has an incredible rank of 6.
PART 3, Odd Loops, Broken Wings, and Dark
Logic Odd
length loops play a role in many methods such as chains, discontinuous nice
loops, and broken wings however, the principle behind broken wings is unique
and is thus a third part to Sudoku Set Logic. Illegal Logic and Odd Length Loops Illegal
logic is any group of sets (or candidates) that has no solution, i.e., there
is no way to arrange the candidates that is allowed by the rules. One type of
illegal logic was shown above. Odd length
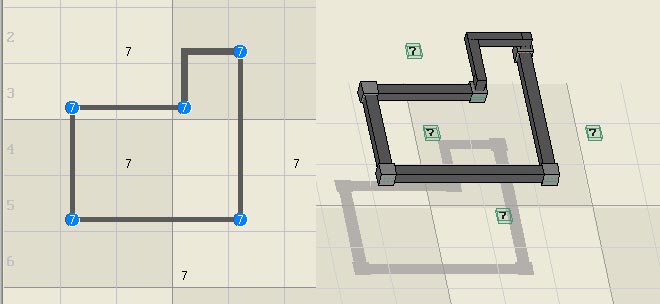
loops of bi-value strong links are also illegal. The length 5 loop below can
contain at most two nodes without double occupancy, thus one set must be
unoccupied. Set loops of any odd length have a rank of minus 1.
Broken Wings The broken wing principle,
introduced by Ron Hagglund and later studied
here, assumes that a valid puzzle cannot contain loops with an odd number
of bi-value strong links (conjugate pairs). To be legal, at least one link must contain at
least one extra candidate, called a guardian. If there is one guardian, it
can be assigned. If there are multiple guardians, eliminations can be
logically deduced. Guardians can be connected to a variety of logic. The lone
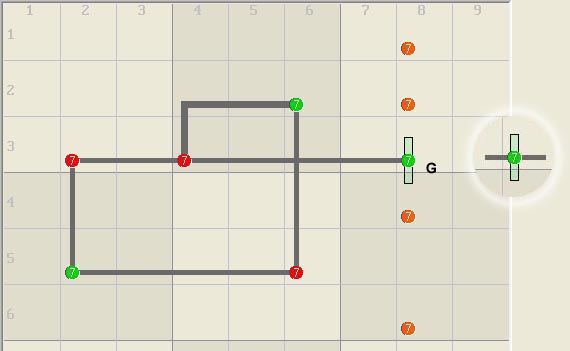
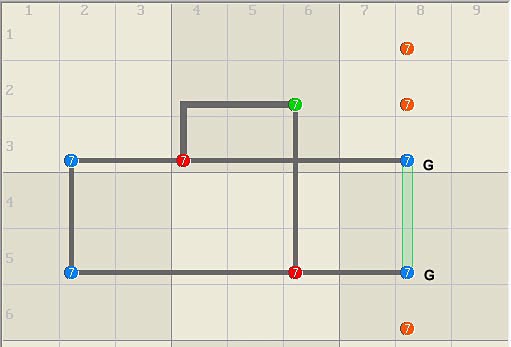
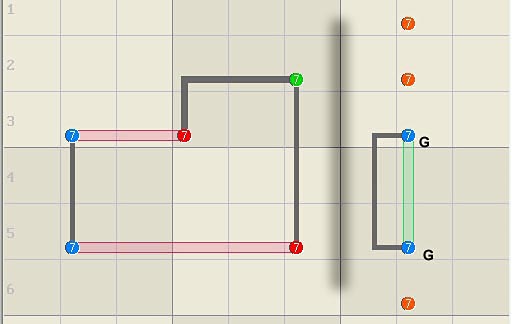
guardian (G) in r3c8 below prevents the logic from being illegal thus it can
be assigned, which then eliminates the orange candidates in column 8.
Eliminated candidates in the structure are red and assigned candidates are
green.
Sets, Broken Wings, and Dark Logic Broken
wings and other illegal logic made of strong sets occur naturally in set
logic. The following is a generalized view of broken wing principles
integrated with Sudoku set theory. The same principles apply to a variety of
logic including deadly patterns and unique rectangles. To
keep track of what's what, the term dark refers to anything
illegal. A dark loop contains the sets
and candidates belonging to illegal logic but not guardians or other logic
that may be in the same sets. In other works, a group of sets may contain a
dark loop and guardians. Defined this way, dark loops have the
following properties: A
dark loop of any size has a rank of minus 1. The
guardians act as a single virtual set that can span rows, columns,
boxes, and digits. The virtual sets can be combined with any other
logic and solved accordingly. A
dark loop can be ignored when solving logic that contains the guardians,
i.e., they are not included in any cover set groups. Thus, dark logic works like
unseen logic that exerts a force on a group of otherwise unconnected
candidates causing them to be logically linked. (Well, its better than
anti-logic). Below
is a two-guardian broken wing. Although neither guardian can be assigned, one
must be true so the linkset in column 8 is always occupied, or rank 0, which
eliminates the red candidates.
The
dark loop's guarantee of one true guardian effectively divides the problem in
two. On the right, the guardians work as a virtual set that forms something
like locked candidates spaning 2 boxes. On the left, rows r3 and r5 are
linksets relative to the dark loop, which can be solved as a discontinuous nice
loop assigning 7r2c6 and eliminating the two red candidates.
Illegal (Dark) Logic and Sets Broken
wings are only one form of illegal logic. Any logic can be used as dark logic
if has no legal arrangement of candidates (permutations). Deadly patterns and
unique rectangles are used in the same way by assuming that valid puzzles
have only one solution. Broken wings and other dark logic require no
assumptions. The
most general definition of dark logic is logic with a negative rank.
A more useful definition is: Any
group of candidates that could be covered by more sets than linksets if
selected candidates were removed. The 'removed' candidates become guardians.
This assumes non-overlap sets. Additional
candidates in linksets do not need to be removed and are not guardians. The
definition does not require all strong links or any conjugate pairs. A simple
example below uses 3 sets and 2 linksets. If the two candidates labeled G are
'removed' then the 6 remaining candidates in rows 3, 5 and columns 2,5,8
become dark. The two G candidates can then be used as a single virtual
set (brown bar) to make a short chain that eliminates candidate 5 in r8c8. Of
course, this example looks a lot like a sashimi.
Sudoku grids contain a lot of unseen dark logic however, most small examples turn out to be other methods or patterns. Dark logic is better suited for difficult puzzles where it might help reduce the size elimination logic because it uses two steps, finding the dark logic and then finding eliminations. Embedded Broken Wings The dark principle applies to
any logic as long as the dark logic nodes do not link to the the rest of the
logic. A more detailed description of and examples of dark
logic can be found in the Odd Loops, Broken
Wings, and dark logic. SUMMARY 1. Every elimination is based on
two groups of sets. The base set group exactly contains a group of
candidates and the link set group contains these candidates as well as
other candidates that are potential eliminations. 2. The number of links minus the
number of base sets is called rank. Rank is a distributed property of the
logic and is uniform everywhere within a logical structure except for
conditions noted below. 3. Rank 0 eliminates any additional
candidates inside of linksets. Common examples include singles, locked
candidates, ALCs, X-wing, swordfish, etc. 4. Rank 1 eliminates any
additional candidates where two linksets overlap. Many Sudoku methods fall
into this category such as finned fish, chains, discontinuous nice loops,
etc. 5. Ranks 2 (or 3) logic requires 3
(or 4) simultaneously overlapping linksets to cause eliminations. 6. Ranks higher than 3 can only
cause eliminations when combined with triplets, described next. 7. A triplet is a single candidate
that connects three sets. A set-triplet has two sets and one linkset, and a
linkset-triplet has two linksets and one set. Triplets "point" in
the direction of the minor link, i.e., the linkset direction of a two set
triplet. The two types of triplets are similar but have different properties. 8. Triplets can divide logic into
high rank and low rank regions and therefore change the number of linksets
that are needed to eliminate a candidate, but this must follow specific
rules. When link triplets point in the direction of a candidate, it may
reduce the number of linksets required to eliminate the candidate.. 9. Set triplets can increase the
number of overlap linksets required to make an elimination if they reduce the
number of true nodes (assigned candidates) guaranteed to be in the set group.
Link-triplets cannot. 10. The area of lower rank caused by a set
triplet usually extends from the triplet's linkset to the first bifurcation
that has independent paths back to the triplet's two sets. For link triplets,
swap the terms set and linkset. 11. The candidate in a set-triplet with an
unconnected linkset can be assigned in rank 0 logic. 12. When triplets are located and aligned
correctly, their effects can be additive however, complex arrangements often
require consideration or additional logical analysis. 13. When two blocks of logic are
(hypothetically) combined, each retains its original rank internally and the
rank of the combined logic is the sum of the individual ranks.
Eliminations can occur when linksets of different blocks overlap based on the
overall rank and triplets used to link blocks. 14. Logic made of, or containing odd length loops of
(strong) sets can contain dark logic, which works similar to broken wings.
Dark logic contains only the sets and nodes that would make illegal logic. 15. A dark loop has a rank of minus 1. A dark loop
can be completely removed from the rest of the logic and all remaining
candidates that were in the removed sets can be placed in a single virtual
set. The virtual set can be used like a normal set with other logic. A
virtual set can have any number of candidates and span rows, columns, and
boxes. 16. After removal, dark loop sets that lost
candidates become linksets and the dark loop can be solved separately, assuming
a solution can be found. |