Introduction to Sudoku
Sudoku
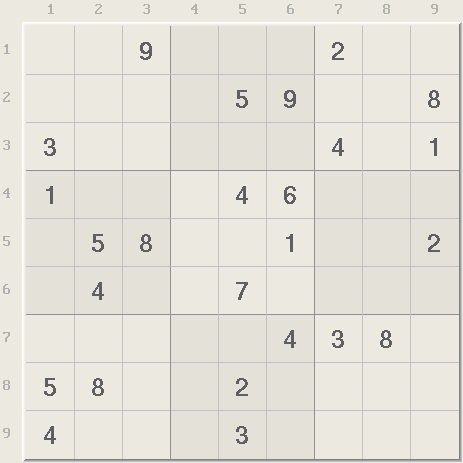
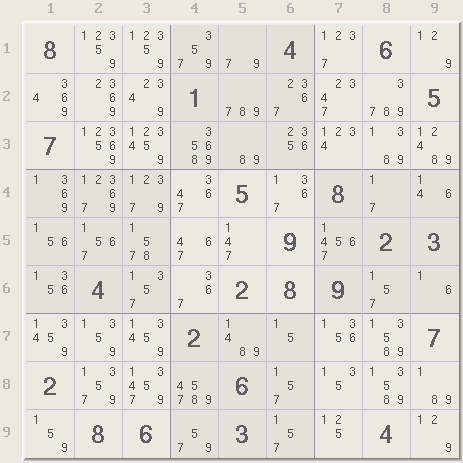
The rules of Sudoku are simple. Sudoku is made of a 9x9 grid with 81 locations or cells that are grouped into 9 rows, 9 columns, and 9 boxes, each with 9 cells. The object is to place the digits 1 to 9 in each cell so that each row, column, and box has only one of each digit. Arithmetic is not used and the 9 digits can be replaced by any 9 symbols. That's it. Below is a typical Sudoku puzzle. If you have Xsudo, you can follow along by clicking on the Xsudo Step links on the right, or open them one time in a separate window.
Counting
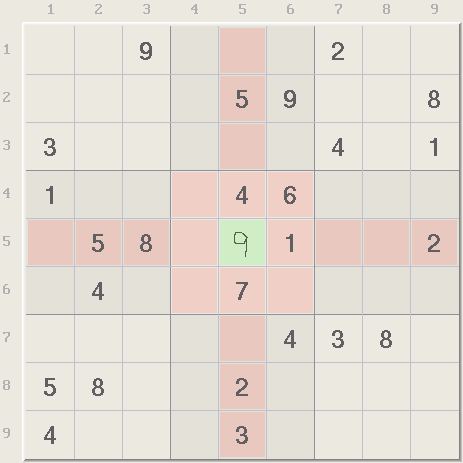
One of the simplest methods for placing digits is to count all the other digits that can see a cell, which means counting all the assigned digits in the cell's row, column, and box. In the example below, all the cells that see the center cell r5c5 (green) are highlighted in red. The red cells contain the digits 12345678 or every digit except 9 so a 9 can be placed in the cell. Of course, one must check all the cells so this was a lucky shot.
Cross Hatching
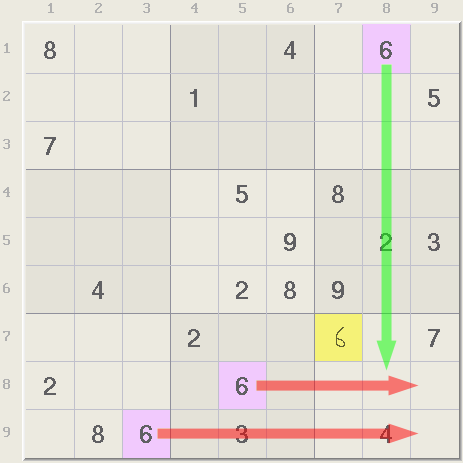
Another method called cross hatching makes use of all the occurrences of a single digit to find a box with only one remaining possibility to place that digit. In the example below, the digit 6 is filling row 8, row 9, and column 8 missing only two locations in the last box. One of the two missed locations is already assigned so the digit 6 can be assigned to the other.
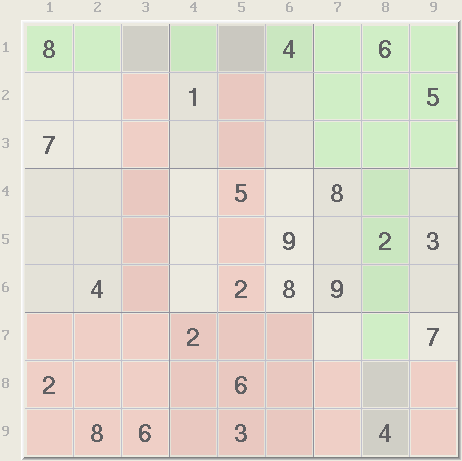
Cross hatching takes many forms and also works for rows and columns. Xsudo has a cross hatching filter to do the work of finding these locations. Below is the same puzzle with a cross hatch applied for the same digit 6, using red and green colors as above. This feature also cross hatches the boxes.
Pencil Marks and Candidates
This seems easy until one considers how many overlapping rows, columns, and boxes there really are, then its time for a better approach. When working on difficult puzzles, one often makes manual pencil marks of which digits can be placed where. For the digit 6 in the previous cross hatch, this is the un-shaded cells. Writing a small 6 in each un-shaded square produces the following. Each pencil mark is called a candidate.
If the candidates for all digits are marked, the grid will look like the puzzle below. Although it's not necessary to mark all candidates at once, most computer programs do this automatically, if you want. From this point, solving Sudoku is a process of eliminating candidates until there is only one left in a cell, row, column, or box, which is then assigned to the solution.
Next:
Basic Sudoku methods using candidates Basic Sudoku Solving Methods