Basic Sudoku Solving Methods
Solving a Sudoku can sometimes require one or more of the many, many known Sudoku solving methods. Below are three of the basic and often used methods. A good introduction and reference for Sudoku methods can be found at Sudopedia.
Hidden Singles
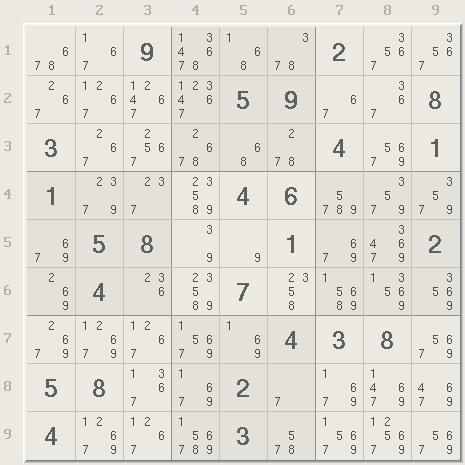
The first technique, called a Naked Single, is the last remaining candidate in a cell. There are two naked singles in the puzzle below, one in row 5, column 5, or r5c5 and the other in r8c6. Naked singles are easy to spot.
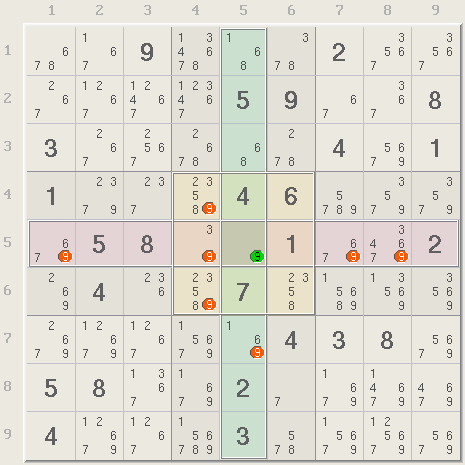
Because the 9 in r5c5 is the only digit in that cell, it must also be the only 9 in row 5, column 5, and the middle box thus all other 9s in these houses can be eliminated. Xsudo will analyze any logic entered by the user In this case, selecting the 9 in r5c5 highlights the Single in green and all the possible eliminations in red. The red 9s can be removed from the puzzle and the green 9 can be assigned.
Hidden Singles
Hidden singles are more difficult to spot because they are the last digits in a row, column, or a box, which means they are mixed with other digits in their cell. Recall the puzzle from the previous page, where cross hatching was used to find the digit 6 in r7c7 (below). The digit 6 was one of two hidden singles in the puzzle. Can you see the other one?
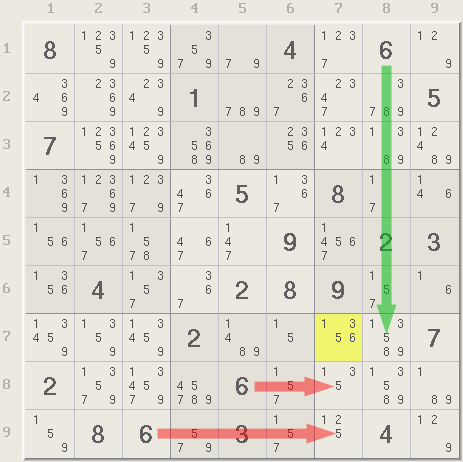
Clicking on digit 6 in r7c7 in Xsudo shows the single in green and the candidates that it eliminates in red. The red candidates can be removed from the puzzle and the green single assigned to the solution.
Locked Candidates
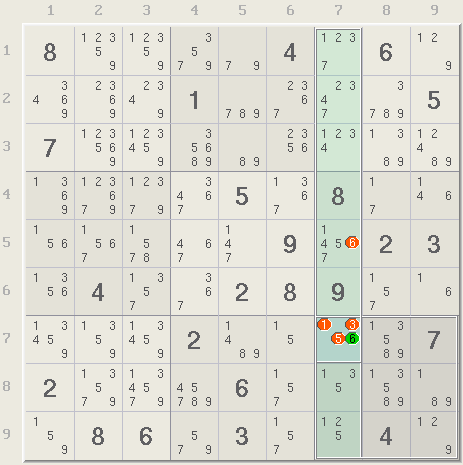
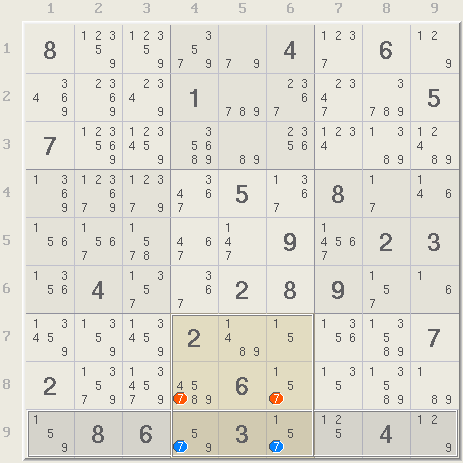
Locked candidates is a more complex move involving two or three candidates instead of one. Row 9 of the same puzzle has two 7s both of which are also in box 8 (light yellow). The box has two additional 7s in row 8. One of the 7s in row 9 must belong to the puzzle's solution, which satisfies the box's requirement for a 7. Therefore, the red 7s in row 8 cannot be in the box and can be eliminated. In effect, the 7s in row 9 are locked in the box. If you are using Xsudo, selecting the two 7s in row 9 will reveal all and make the eliminations.
How To Find X-Wings (a fish!)
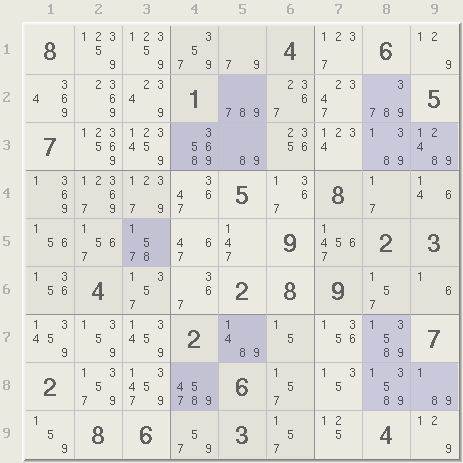
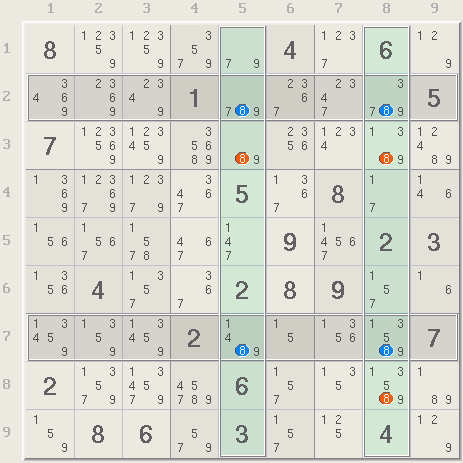
From the webpage, an X-Wing is a group of 4 candidates, or 2 pairs of candidates where a) each pair are the only digits in a row or column, and b) the two pairs line up in the opposite direction, i.e., if the pairs are in rows then they line up in the columns. X-Wings are not easy to spot but can be found using a candidate filter to highlight all the cells with a particular candidate. Below is Xsudo's candidate filter for digit 8, where it's easy that there are only two blue squares in rows 2 and 7, and these squares line up in columns 5 and 8.
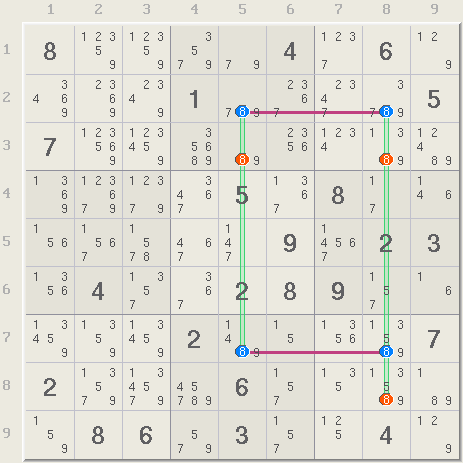
Confirming the X-Wing
An X-Wing is a more powerful method involving 4 candidates in two rows. Both rows have two candidates and all four candidates are also in two overlapping columns (green). The argument here is that one of the two 8s in each black row must belong to the solution (be true). Whichever two 8s are true, they are also in the two green columns thus no other 8s can be elsewhere in the columns. Thus all the red 8s can be removed. X-Wings take skill to find however, Xsudo's background logic will recognize the X-Wing when the candidates are selected.
Looking at Xsudo's Logic
As logic is entered, Xsudo continues to calculate all the logical possibilities looking for eliminations and assignments, and displays the results. When the four candidates of the X-Wing are entered, Xsudo's logic will look like this. The solid dark lines are the sets and the light transparent lines are the links.
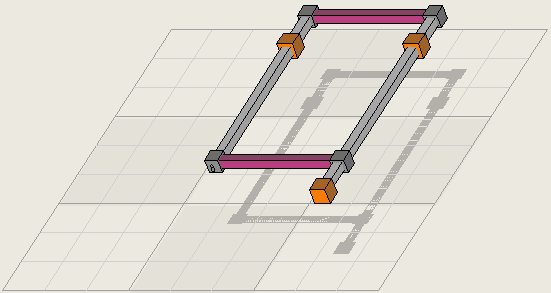
Looking at Xsudo's Logic in 3D
In three dimensions, the X-Wing looks like this, shown using Xsudo's 3D mode. The 3D mode in Xsudo is fully functional and allows editing and the application of most features.
A Logical Way of Reasoning
One simple way of reasoning can be seen by looking at the X-Wing diagram again. In Sudoku, each row, column, and box must have exactly one of every digit thus we can reason that:
· The two black rows have four 8s (blue color), two of which must be true.
· Since the green links contain all blue 8s, they must contain two blue 8s that are true.
· Since the green links already contain two true-blue 8s, none of the other (orange) eights can be true.
· The red 8s can thus be removed from the puzzle.
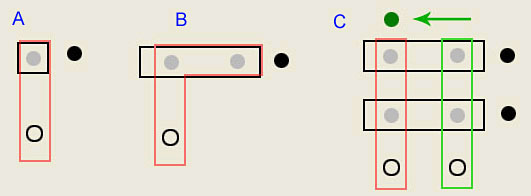
This will always be true if the green links contain all the 8s in the black sets and the number of links equals the number of black sets. As shown below, this is true for Singles (A), Locked Candidates (B), and the X-Wing (C). This simple idea is the basic idea behind a more general approach to Sudoku.